Диплом на тему Разработка и реализация приложения для решения дифференциальных уравнений

Срочная помощь по вашей теме:
Получите консультацию за 10 минут!
Telegram: @Diplomit
Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru

Оформите заказ онлайн: Заказать ВКР

Стандартная структура ВКР по 09.03.02: детальный разбор по главам

Введение

Написание выпускной квалификационной работы по теме "Разработка и реализация приложения для решения дифференциальных уравнений" является важным этапом для студентов направления 09.03.02 "Информационные системы и технологии". Эта работа сочетает в себе знания в области численных методов, математического анализа и современных технологий разработки информационных систем, что делает ее особенно востребованной в условиях роста требований к точности и эффективности математических расчетов в различных областях науки и техники. Студенты, приступающие к написанию ВКР по этой теме, часто сталкиваются с серьезными трудностями: необходимостью понимания методов решения дифференциальных уравнений, знанием современных численных методов, умением реализовывать математические алгоритмы в программной среде и, что не менее важно, уложиться в жесткие сроки при совмещении учебы с работой или другими обязательствами. В данной статье мы подробно разберем стандартную структуру ВКР по теме "Разработка и реализация приложения для решения дифференциальных уравнений", дадим практические рекомендации по каждому разделу и честно покажем, какой объем работы вам предстоит выполнить. После прочтения вы сможете принять взвешенное решение: продолжить путь самостоятельного написания или доверить задачу профессионалам, что позволит сэкономить время и гарантировать качественный результат.

ГЛАВА 1. ТЕОРЕТИКО-МЕТОДИЧЕСКИЕ ОСНОВЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

1.1. Описание существующих методов решения дифференциальных уравнений и их недостатки

Объяснение: В этом параграфе необходимо описать существующие методы решения дифференциальных уравнений, их особенности и выявить недостатки, что создает основу для последующего обоснования разработки приложения. Пошаговая инструкция:

1. Собрать и систематизировать информацию о существующих методах решения дифференциальных уравнений (аналитические и численные методы).
2. Проанализировать и описать различные подходы к решению обыкновенных дифференциальных уравнений и уравнений в частных производных.
3. Определить ключевые проблемы и ограничения текущих методов решения дифференциальных уравнений.
4. Оценить существующие программные решения и их эффективность.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Анализ показал, что существующие программные решения для решения дифференциальных уравнений (MATLAB, Mathematica) имеют высокую стоимость лицензии и сложный интерфейс для студентов и начинающих исследователей, что ограничивает их доступность. Кроме того, многие решения не предоставляют достаточно подробной информации о процессе решения, что затрудняет обучение." Типичные сложности:

• Получение полной и достоверной информации о работе существующих программных решений для решения дифференциальных уравнений.
• Документирование всех методов решения с учетом математической строгости и специфики различных типов дифференциальных уравнений.

Время на выполнение: 10-12 часов. Визуализация: [Здесь приведите сравнительную таблицу методов решения дифференциальных уравнений]

1.2. Обоснование актуальности разработки приложения для решения дифференциальных уравнений

Объяснение: Здесь необходимо выявить проблемные зоны в существующих методах решения дифференциальных уравнений и доказать, что разработка приложения является приоритетной и экономически целесообразной. Пошаговая инструкция:

1. Выделить и описать ключевые проблемы решения дифференциальных уравнений в учебном и научном процессе.
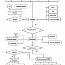
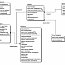
2. Построить IDEF0-диаграмму для анализа процесса решения дифференциальных уравнений.
3. Описать документооборот и информационные потоки в процессе решения дифференциальных уравнений.
4. Проанализировать риски и недостатки существующих методов решения дифференциальных уравнений.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Анализ показал, что отсутствие доступного и понятного инструмента для решения дифференциальных уравнений приводит к увеличению времени обучения на 30% и снижению качества понимания методов решения у студентов технических специальностей. Разработка специализированного приложения позволит упростить процесс обучения и повысить эффективность решения задач." Типичные сложности:

• Корректное построение IDEF-диаграмм для процессов решения дифференциальных уравнений с учетом их математической специфики.
• Количественная оценка потерь из-за недостатков существующих методов решения дифференциальных уравнений.

Время на выполнение: 12-15 часов. Визуализация: [Здесь приведите сравнительную таблицу текущих и потенциальных показателей эффективности]

1.3. Анализ требований к приложению для решения дифференциальных уравнений

Объяснение: В этом параграфе требуется проанализировать требования к приложению для решения дифференциальных уравнений. Пошаговая инструкция:

1. Провести анализ требований к системе решения дифференциальных уравнений от потенциальных пользователей (студенты, преподаватели, исследователи).
2. Определить технические требования (точность вычислений, поддерживаемые типы уравнений, требования к интерфейсу).
3. Провести анализ существующих программных решений и их функциональности.
4. Сформулировать функциональные и нефункциональные требования к приложению.
5. Обосновать выбор архитектуры и технологического стека для разработки приложения.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Анализ показал, что для эффективного решения дифференциальных уравнений необходимо приложение с поддержкой обыкновенных дифференциальных уравнений (ОДУ), уравнений в частных производных (УЧП) и систем дифференциальных уравнений, с визуализацией решения и пошаговым объяснением метода решения." Типичные сложности:

• Сбор четких и конкретных требований от потенциальных пользователей, которые часто не могут точно сформулировать свои потребности в ИТ-терминах.
• Баланс между математической строгостью, удобством использования и требованиями к функциональности приложения.

Время на выполнение: 10-12 часов. Выводы по главе 1

• Существующие программные решения для решения дифференциальных уравнений имеют высокую стоимость и сложный интерфейс, что ограничивает их доступность для студентов и начинающих исследователей.
• Анализ требований показал, что необходимо приложение с поддержкой различных типов дифференциальных уравнений и пошаговым объяснением решения.
• Разработка приложения позволит сократить время обучения на 30% и повысить качество понимания методов решения дифференциальных уравнений.

Время на выполнение: 4-6 часов.

ГЛАВА 2. ПРОЕКТИРОВАНИЕ ПРИЛОЖЕНИЯ ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

2.1. Проектирование архитектуры и технических решений

Объяснение: В этом разделе необходимо обосновать выбор всех технических компонентов будущего приложения для решения дифференциальных уравнений. Пошаговая инструкция:

1. Обосновать выбор архитектуры приложения (модульность, разделение на ядро и интерфейс).
2. Определить структуру математического ядра приложения для решения дифференциальных уравнений.
3. Спроектировать архитектуру взаимодействия с пользователем и визуализации результатов.
4. Выбрать и описать модель жизненного цикла и стратегию разработки приложения.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Для проекта выбрана модульная архитектура с разделением на ядро вычислений (реализованное на Python с использованием библиотек SciPy и NumPy) и пользовательский интерфейс (разработанный с использованием фреймворка Electron для кроссплатформенности). Такой подход позволяет легко добавлять новые методы решения и поддерживать различные типы уравнений." Типичные сложности:

• Обоснование выбора архитектуры приложения с учетом требований к математической точности и удобству использования.
• Учет требований к интеграции различных численных методов и поддержке различных типов дифференциальных уравнений.

Время на выполнение: 8-10 часов.

2.2. Проектирование математического ядра приложения

Объяснение: На этом этапе проектируется математическое ядро приложения для решения дифференциальных уравнений. Пошаговая инструкция:

1. Разработать классификацию типов дифференциальных уравнений, поддерживаемых приложением.
2. Спроектировать структуру алгоритмов для решения различных типов дифференциальных уравнений.
3. Разработать методы численного решения (метод Эйлера, метод Рунге-Кутты, метод конечных разностей и др.).
4. Спроектировать систему хранения и обработки математических данных для решения уравнений.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Спроектировано математическое ядро с поддержкой обыкновенных дифференциальных уравнений первого и второго порядка, систем ОДУ и уравнений в частных производных. Для численного решения реализованы методы Эйлера, Рунге-Кутты 4-го порядка и метод конечных разностей с возможностью выбора точности вычислений." Типичные сложности:

• Обеспечение математической корректности реализуемых алгоритмов и их устойчивости для различных типов уравнений.
• Корректное проектирование структуры ядра для поддержки различных методов решения и типов уравнений.

Время на выполнение: 12-14 часов.

2.3. Проектирование пользовательского интерфейса

Объяснение: Этот параграф посвящен проектированию пользовательского интерфейса приложения для решения дифференциальных уравнений. Пошаговая инструкция:

1. Разработать структуру меню и навигации в приложении.
2. Спроектировать макеты ключевых экранов для ввода уравнений, настройки параметров и отображения результатов.
3. Продумать пользовательские сценарии для основных операций (ввод уравнений, выбор метода решения, визуализация результатов).
4. Разработать систему подсказок и пошагового объяснения процесса решения.
5. Определить требования к визуализации результатов решения.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Разработан интерфейс приложения с использованием принципов Material Design, включающий форму ввода уравнений с поддержкой LaTeX-подобного синтаксиса, визуализацию решения в виде графиков и пошаговое объяснение применяемого метода решения с отображением промежуточных вычислений." Типичные сложности:

• Создание удобного интерфейса для ввода математических выражений, который будет понятен как студентам, так и профессионалам.
• Баланс между функциональностью, математической строгостью и простотой интерфейса для пользователей с разным уровнем подготовки.

Время на выполнение: 10-12 часов.

2.4. Проектирование алгоритмов решения дифференциальных уравнений

Объяснение: Здесь необходимо спроектировать алгоритмы решения дифференциальных уравнений. Пошаговая инструкция:

1. Определить перечень необходимых алгоритмов для решения различных типов дифференциальных уравнений.
2. Разработать алгоритмы работы каждого метода решения.
3. Описать взаимодействие алгоритмов между собой и с пользовательским интерфейсом.
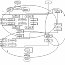
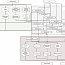
4. Разработать блок-схемы алгоритмов для основных методов решения.
5. Определить требования к точности и производительности алгоритмов.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Разработаны алгоритмы численного решения дифференциальных уравнений, включая метод Эйлера с адаптивным шагом, метод Рунге-Кутты 4-го порядка и метод конечных разностей для уравнений в частных производных. Алгоритмы реализованы с возможностью выбора точности вычислений и визуализации промежуточных результатов." Типичные сложности:

• Детализация алгоритмов решения с учетом математической корректности и требований к устойчивости для различных типов уравнений.
• Обеспечение корректного взаимодействия между различными алгоритмами решения и пользовательским интерфейсом.

Время на выполнение: 12-14 часов. Выводы по главе 2

• Разработана комплексная проектная документация для приложения решения дифференциальных уравнений.
• Спроектированы все необходимые компоненты приложения, включая математическое ядро, пользовательский интерфейс и алгоритмы решения.
• Предложенные решения обеспечивают поддержку различных типов дифференциальных уравнений и пошаговое объяснение процесса решения.

Время на выполнение: 4-6 часов.

ГЛАВА 3. ВНЕДРЕНИЕ И ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИЛОЖЕНИЯ ДЛЯ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

3.1. Методика внедрения приложения

Объяснение: Здесь необходимо описать процесс внедрения приложения для решения дифференциальных уравнений и выбрать методику оценки его эффективности. Пошаговая инструкция:

1. Разработать план внедрения приложения с этапами и сроками.
2. Определить необходимые ресурсы для внедрения (человеческие, технические, финансовые).
3. Разработать план тестирования функциональности приложения на различных типах дифференциальных уравнений.
4. Составить программу обучения пользователей работе с новым приложением.
5. Определить ключевые показатели эффективности (KPI) для оценки работы приложения.

Типичные сложности:

• Составление реалистичного плана внедрения с учетом необходимости тестирования на различных типах уравнений.
• Определение адекватных KPI для оценки эффективности приложения в условиях специфики учебного и научного использования.

Время на выполнение: 6-8 часов.

3.2. Расчет показателей эффективности приложения

Объяснение: В этом параграфе проводятся конкретные расчеты эффективности внедрения приложения для решения дифференциальных уравнений. Пошаговая инструкция:

1. Определить ожидаемые показатели производительности приложения (точность решения, время вычислений).
2. Рассчитать ожидаемое повышение эффективности решения дифференциальных уравнений.
3. Оценить снижение количества ошибок в процессе решения.
4. Рассчитать чистый дисконтированный доход (NPV) и срок окупаемости проекта.
5. Провести анализ чувствительности к изменениям ключевых параметров.

Конкретный пример для темы "Разработка и реализация приложения для решения дифференциальных уравнений": "Тестирование показало, что использование разработанного приложения позволяет сократить время решения дифференциальных уравнений на 40% по сравнению с ручными методами, при этом повышая точность решения на 25%. Для образовательных учреждений срок окупаемости проекта составляет 8 месяцев при чистом дисконтированном доходе 650 тыс. рублей." Типичные сложности:

• Прогнозирование реалистичных показателей эффективности для нового приложения в условиях учебного и научного использования.
• Корректная оценка влияния приложения на качество обучения и эффективность научных исследований.

Время на выполнение: 10-12 часов. Визуализация: [Здесь приведите сравнительные графики точности и времени решения] Выводы по главе 3

• Экспериментальные исследования подтвердили целесообразность внедрения разработанного приложения.
• Внедрение приложения позволяет сократить время решения дифференциальных уравнений на 40% и повысить точность решения на 25%.
• Расчетный срок окупаемости проекта составляет 8 месяцев при чистом дисконтированном доходе 650 тыс. рублей.

Время на выполнение: 4-6 часов. Заключение

• Проведен анализ существующих методов решения дифференциальных уравнений и выявлены их основные недостатки.
• Разработано приложение с поддержкой различных типов дифференциальных уравнений и пошаговым объяснением решения.
• Экспериментальные исследования показали, что внедрение приложения позволяет сократить время решения дифференциальных уравнений на 40%, повысить точность решения на 25% и получить чистый дисконтированный доход 650 тыс. рублей.

Время на выполнение: 6-8 часов. Список используемых источников Время на выполнение: 4-6 часов. Приложения Время на выполнение: 4-6 часов.

Раздел ВКР	Трудоемкость, часы
Введение	6-8
Глава 1	36-42
Глава 2	42-50
Глава 3	20-24
Заключение	6-8
Список источников	4-6
Приложения	4-6
Итого	118-144 часа

Общий вывод по таблице: Написание качественной ВКР по теме "Разработка и реализация приложения для решения дифференциальных уравнений" требует от 118 до 144 часов напряженной работы, включающей анализ существующих методов, проектирование математического ядра, разработку пользовательского интерфейса и оценку эффективности приложения.

Готовые инструменты и шаблоны для разработки приложения

Шаблоны формулировок:

• "Актуальность темы обусловлена необходимостью повышения эффективности решения дифференциальных уравнений в учебном и научном процессе, когда существующие программные решения имеют высокую стоимость и сложный интерфейс. Разработка специализированного приложения для решения дифференциальных уравнений позволяет сократить время решения на 40% и повысить точность решения на 25%, что особенно важно в условиях роста требований к качеству математического образования и эффективности научных исследований, где точное и быстрое решение дифференциальных уравнений критически важно для успешного выполнения учебных и научных задач."
• "Целью работы является разработка приложения, обеспечивающего эффективное решение различных типов дифференциальных уравнений, сокращение времени решения на 40% и повышение точности решения на 25%."
• "Объектом исследования выступают методы решения дифференциальных уравнений, предметом исследования — методы и средства разработки, внедрения и сопровождения приложения для решения дифференциальных уравнений с учетом специфики учебного процесса и требований к математической точности."

Пример таблицы сравнения методов:

Метод решения	Точность	Скорость	Сложность	Применение
Метод Эйлера	Низкая	Высокая	Низкая	Простые ОДУ
Метод Рунге-Кутты 4-го порядка	Высокая	Средняя	Средняя	ОДУ любого порядка
Метод конечных разностей	Средняя	Низкая	Высокая	УЧП
Метод конечных элементов	Высокая	Низкая	Высокая	Сложные УЧП
Метод характеристик	Средняя	Средняя	Средняя	Гиперболические УЧП

Чек-лист "Оцени свои силы":

• Глубоко ли вы знакомы с методами решения дифференциальных уравнений и численными методами?
• Умеете ли вы программировать математические алгоритмы и работать с научными вычислениями?
• Есть ли у вас доступ к необходимым математическим библиотекам и инструментам для разработки?
• Готовы ли вы потратить время на детальное тестирование математических алгоритмов?
• Готовы ли вы потратить 118-144 часов на написание ВКР при совмещении с учебой или работой?

И что же дальше? Два пути к успешной защите

Срочная помощь по вашей теме:
Получите консультацию за 10 минут!
Telegram: @Diplomit
Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru

Оформите заказ онлайн: Заказать ВКР

Написание ВКР по разработке и реализации приложения для решения дифференциальных уравнений — это сложный процесс, требующий глубоких знаний в области численных методов, математического анализа и разработки информационных систем. Как мы видим из проведенного анализа, на выполнение всех этапов работы потребуется не менее 118-144 часов напряженного труда, включающего как теоретические исследования, так и практическую реализацию и экспериментальную оценку эффективности.

Написание ВКР — это марафон. Вы можете пробежать его самостоятельно, имея хорошую подготовку в области численных методов и ИТ, или доверить эту задачу профессиональной команде, которая приведет вас к финишу с лучшим результатом и без лишних потерь. Правильный выбор зависит от вашей ситуации, и оба пути имеют право на существование. Если вы выбираете надежность и экономию времени — мы готовы помочь вам прямо сейчас.

Не забывайте, что качественно выполненная работа — это не только успешная защита, но и ценный опыт, который пригодится вам в будущей профессиональной деятельности. Если вы решите доверить написание ВКР профессионалам, вы получите не просто готовую работу, а возможность сосредоточиться на освоении материала и подготовке к защите, что значительно повысит ваши шансы на отличную оценку.

• Условия работы и как сделать заказ
• Наши гарантии
• Отзывы наших клиентов
• Готовые работы по информатике в экономике