Программа для построения раскраски графа общего вида с использованием эвристических методов, дипломная работа про программированию
Получите бесплатно демо-версию Демо-версия - дипломная работа, в котрой удалена часть текста, рисунков, таблиц.Посмотреть все услуги дипломной работы на электронную почту.
Введите адрес электронной почты и нажмите "Отправить"
Разработка сайта салона красоты с возможностью записи клиентов6 120 ₽
Разработка автоматизированной системы учета товаров и продаж для торговой компании9 200 ₽
Разработка корпоративной вычислительной сети с использованием технологии VPN, диплом по сетям7 000 ₽
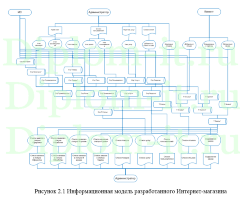
Применение DLP-систем как инструмента обеспечения информационной безопасности компании, диплом по защите информации8 900 ₽9 900 ₽Описание
Работа выполнена и сдана в 2017 году.
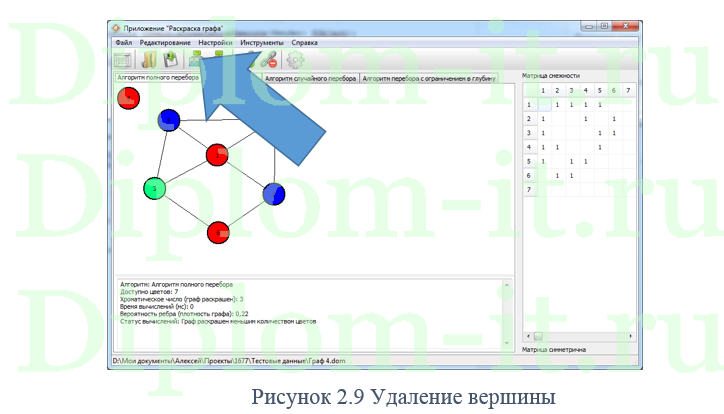
В выпускной квалификационной работе бакалавра в соответствии с заданием разработано программное обеспечение для построения раскраски графа общего вида с использованием эвристических методов.
Проведено предпроектное исследование, в котром выделана задача работы и практическое примерении теории раскраски графов.
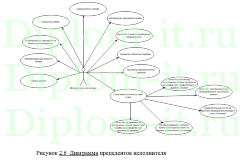
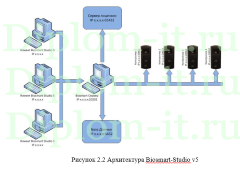
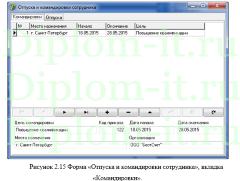
Описаны алгоритмы раскраски графов, проведено их сравнение. Разработан алгоритм работы программы, обоснован выбор аржитектуры и средств разработки, описана структура ее классов и описано руководство пользователя.
Приложен акт внедрения результатов данной выпускной квалификационной работы на ФКП образовательном учреждении № 98.
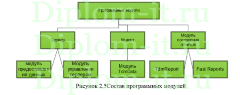
ВКР включает 64 страницы, имеет 6 таблиц, 34 рисунка.
Широкое внедрение ЭВМ и систем управления во все сферы деятельности человека и усложнение задач, которые эти системы решают, постоянно требует совершенствования существующих методов и создания новых алгоритмов логического проектирования цифровых устройств. Логическое проектирование тут подразумевается в широком смысле, включая не только статику систем, т.е. их функциональные связи и структуру, но и изучение динамики структуры, а также на уровне переходных процессов, связанных с постоянными и временными параметрами элементов. Поэтому все исследования, направленные на улучшение методики логического проектирования цифровых устройств, поддерживающих выполнение процедуры проектирования, оптимизацию базовых характеристик ЦУ, а также уменьшение времени и цены разработки никогда не потеряют своей актуальности.
В случае применения моделей нечетких графов и гиперграфов конкретный научный интерес имеют задачи нахождения их типичных параметров, а также задачи, связанные с их окраской.
Изначально нечеткая окраска нечеткого графа связана с понятием А-уровня нечеткого множества и его делением на нечеткие графы. Тут по А-уровнем нечеткого графа ставится четкий суграф, где вершины смежны тогда и только тогда, когда степень смежности вершин в начальном графе меньше параметра А (0<А<1). Тогда задача окраски заключается в классическом окрашивании графов А-уровня, т.е. в поиске наименьшего числа красок (хроматического числа) для графа А-уровня, когда смежным вершинам даются разные цвета. Дальнейший подход к окраске нечетких графов связывается с понятия стабильности произвольного числа вершин нечеткого графа. Под стабильностью вершин понимается величина, обратно пропорциональная наименьшему значению степени смежности всех пар входящих в него вершин. Тогда нечеткому графу ставится в соответствие нечеткое хроматическое множество, выражающее максимальную степень делимости вершин при окраске графа в указанное число красок.
Изначально подход к нечеткой окраске нечеткого гиперграфа состоит в том, что, описывая нечеткий гиперграф как совокупность четкого гиперграфа, переходим к пониманию окраски гиперграфа как делению множества вершин на подмножества так, что любое ребро пересекается с двумя из этих подмножеств минимум. Проще говоря, все вершины гиперграфа, принадлежащие одному ребру, окрашиваются не менее 2 цветами. Последующий проход рассматривает нечеткий гиперграф как совокупность нечеткого графа, окрашивая гиперграф как разбиение множества вершин на подмножества таким образом, что вершины гиперграфа, принадлежащие одному ребру, окрашиваются разными цветами.
Цель ВКР заключена в создании ПО для раскраски графа общего вида с применением эвристических методов.
Основными задачами проекта становятся:
- Анализ алгоритмов раскраски графов;
- Выбор средств разработки;
- Разработка руководства пользователя программы.
Работа также включает программное обеспечение на языке Delphi .
Характеристики
Год | 2017 |
Программа с исходниками | Да, Delphi |
Никогда не думала, что буду обращаться к кому-то за написанием дипломной работы, но в связи с очень высокими требованиями научного руководителя решила на свой страх и риск обратиться сюда. Спасибо данной компании за мои восстановленные нервы и ментальное здоровье. Всегда на связи, понравилось, что все правки, которые возникали у научного-все вносилось и причем без доплаты, вопросов. Вошли в положение и написали все достаточно быстро, причем учли то, что ранее я сама уже написала. За цену отдельный лайк.
Отличный сервис, буквально выручил меня! Как-то туго у меня учеба шла в этом году, дипломную сам написать не смог. Обратился сюда, рассказал, что нужно сделать. В итоге, получил отличный балл! Большое вам спасибо, что выручили в сложной ситуации. Кстати, взяли совсем немного, особенно, если учитывать, как хорошо сделали мою работу, определенно рекомендую.
Из-за высокой загруженности не успевал написать дипломную по программированию самостоятельно, поэтому обратился в эту компанию. Ребята очень отзывчивые, договорились обо всём быстро. Антиплагиат прошел без проблем, однако пришлось столкнуться с такой проблемкой, как небольшие замечания от руководителя, но с этим решили тоже быстро, внесли коррективы, причем без доплат, и все остались довольны.
Во-первых, сразу же оценила, что на мои письма быстро отвечают, а не морозятся, заставляя понервничать, а во-вторых, с самой работой справились на все 5, как и оценил преподаватель) Даже исправлять ничего не пришлось, чему я была приятно удивлена. Со всеми бы так проходило сотрудничество)
Практически вся наша группа заказывала дипломные работы здесь. Привлекли адекватные цены, качество работы, высокая степень уникальности. Также презентация и доклад входят в комплект работы, их не нужно дополнительно оплачивать, как в других компаниях. Лично от моей работы руководитель был в восторге, очень хвалил, в итоге защитилась очень хорошо.
