Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР КФУ
Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля
Пошаговое руководство по написанию ВКР КФУ для направления 01.03.02 «Прикладная математика и информатика»
Введение: Важность исследования вертикальной динамики грузовых автомобилей
Написание выпускной квалификационной работы по теме "Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля" — это сложная задача, требующая глубоких знаний в области теоретической механики, теории колебаний и численных методов. Студенты КФУ, обучающиеся по направлению 01.03.02 «Прикладная математика и информатика», часто сталкиваются с проблемой нехватки времени и недостаточного опыта в создании математических моделей динамики подвески, что делает выполнение такой работы крайне трудоемким процессом.
Математическое моделирование вертикальных колебаний грузовых автомобилей открывает новые возможности для повышения комфорта водителя, снижения износа компонентов транспортного средства и улучшения устойчивости на дороге. Двухосные грузовые автомобили, составляющие основу коммерческого транспорта, испытывают значительные вертикальные нагрузки при движении по неровным дорогам, что требует тщательного анализа динамики колебаний для оптимизации параметров подвески. Однако создание точных математических моделей для таких систем требует учета сложных взаимодействий между кузовом, колесами и дорожным покрытием, а также нелинейных свойств амортизаторов и пружин.
В этой статье мы подробно разберем стандартную структуру ВКР КФУ по вашей специальности, выделим ключевые этапы математического и компьютерного моделирования динамики вертикальных колебаний двухосного грузового автомобиля и покажем типичные сложности, с которыми сталкиваются студенты. Вы получите конкретные примеры, шаблоны формулировок и чек-лист для оценки своих возможностей. После прочтения станет ясно, насколько реалистично выполнить такую работу самостоятельно в установленные сроки.
Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР КФУ
Детальный разбор структуры ВКР: почему это сложнее, чем кажется
Стандартная структура ВКР КФУ по направлению 01.03.02 «Прикладная математика и информатика» включает несколько ключевых разделов, каждый из которых имеет свои особенности и подводные камни при работе с математическими моделями динамики вертикальных колебаний двухосных грузовых автомобилей.
Введение - что здесь писать и почему студенты "спотыкаются"?
Цель раздела: Обосновать актуальность темы, сформулировать цель и задачи исследования, определить объект и предмет работы.
Пошаговая инструкция:
- Актуальность: Обоснуйте, почему математическое моделирование вертикальных колебаний двухосных грузовых автомобилей важно для современных транспортных систем.
- Степень разработанности: Проведите анализ существующих исследований в области математического моделирования динамики подвески автомобилей.
- Цель исследования: Сформулируйте четкую цель (например, "Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля для оптимизации параметров подвески").
- Задачи: Перечислите 4-6 конкретных задач, которые необходимо решить для достижения цели.
- Объект и предмет исследования: Укажите объект (процесс вертикальных колебаний двухосного грузового автомобиля) и предмет (математическая модель).
- Методы исследования: Перечислите методы математического моделирования, теории колебаний и программирования, которые будут использованы.
- Научная новизна и практическая значимость: Объясните, что нового вносит ваша работа.
Конкретный пример для темы "Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля":
Актуальность: "В условиях увеличения грузопотоков и ужесточения требований к комфорту и безопасности водителей актуальность исследования вертикальной динамики грузовых автомобилей значительно возросла. Согласно исследованиям International Journal of Heavy Vehicle Systems (2024), нерациональные параметры подвески двухосных грузовых автомобилей приводят к увеличению усталости водителя на 25-30% и повышению износа компонентов транспортного средства на 20-25%. Однако существующие модели часто не учитывают полной динамики взаимодействия кузова, колес и дорожного покрытия, особенно в условиях переменной загрузки, что создает потребность в разработке комплексной математической модели, способной точно предсказывать поведение двухосного грузового автомобиля при вертикальных колебаниях. Это особенно важно в свете требований к повышению комфорта водителей и снижению эксплуатационных затрат на техническое обслуживание грузового автопарка."
Типичные сложности:
- Трудно обосновать научную новизну, так как многие методы моделирования хорошо изучены
- Много времени уходит на подбор и анализ современных источников по теории колебаний за последние 3-5 лет
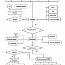
[Здесь приведите схему: "Схема двухосного грузового автомобиля с подвеской"]
Глава 1: Теоретические основы моделирования вертикальной динамики грузовых автомобилей
Цель раздела: Показать глубину понимания предметной области и обосновать выбор методов решения.
Пошаговая инструкция:
- Изучите основные понятия теории колебаний: собственные частоты, демпфирование, резонанс.
- Проанализируйте особенности двухосных грузовых автомобилей: распределение массы, типы подвески, динамические характеристики.
- Исследуйте методы моделирования подвески: линейные и нелинейные модели, дискретные и континуальные подходы.
- Выявите недостатки и ограничения существующих моделей вертикальной динамики грузовых автомобилей.
- Обоснуйте выбор уровня детализации математической модели для вашего исследования.
Конкретный пример:
В этой главе можно привести сравнительный анализ различных моделей подвески для грузовых автомобилей:
| Тип модели | Преимущества | Недостатки | Подходит для |
|---|---|---|---|
| Модель с одной степенью свободы | Простота, аналитическое решение | Низкая точность, не учитывает взаимодействие осей | Быстрая оценка собственной частоты |
| Модель с двумя степенями свободы | Учет взаимодействия передней и задней подвески | Не учитывает продольные колебания | Анализ вертикальной динамики |
| Модель с четырьмя степенями свободы | Высокая точность, учет продольных колебаний | Сложность, требует численного решения | Глубокий анализ динамики |
| Ваше решение | Баланс между точностью и сложностью | Требует тщательной настройки | Моделирование двухосного грузовика |
Типичные сложности:
- Студенты часто поверхностно изучают теорию колебаний
- Сложность в понимании нелинейных свойств амортизаторов
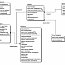
[Здесь приведите схему: "Силы, действующие на двухосный грузовой автомобиль при вертикальных колебаниях"]
Глава 2: Математические основы и уравнения вертикальной динамики двухосного грузового автомобиля
Цель раздела: Представить математическую основу для разрабатываемой модели и обосновать выбор методов.
Пошаговая инструкция:
- Определите систему координат и обозначения для моделирования вертикальных колебаний.
- Разработайте математическую модель вертикальных колебаний двухосного грузового автомобиля.
- Выберите и опишите уравнения движения с учетом особенностей подвески.
- Проведите теоретический анализ свойств и устойчивости модели.
- Приведите примеры решения конкретных задач вертикальной динамики.
Конкретный пример:
Для моделирования вертикальных колебаний двухосного грузового автомобиля:
Уравнения движения (модель с двумя степенями свободы):
m · d²z/dt² + c_f · (dz/dt - dz_f/dt) + c_r · (dz/dt - dz_r/dt) + k_f · (z - z_f - h_f) + k_r · (z - z_r - h_r) = 0
I_y · d²θ/dt² + a · k_f · (z - z_f - h_f) - b · k_r · (z - z_r - h_r) + a · c_f · (dz/dt - dz_f/dt) - b · c_r · (dz/dt - dz_r/dt) = 0
где m - масса кузова, I_y - момент инерции относительно поперечной оси, z - вертикальное смещение центра масс, θ - угол продольного наклона, k_f, k_r - жесткость передней и задней подвески, c_f, c_r - коэффициенты демпфирования
Частотное уравнение:
det(K - ω²M) = 0
где K - матрица жесткости, M - матрица масс, ω - круговая частота
Типичные сложности:
- Ошибки в выводе уравнений движения для модели с двумя степенями свободы
- Сложность в учете нелинейных свойств амортизаторов
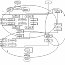
[Здесь приведите схему: "Математическая модель двухосного грузового автомобиля"]
Глава 3: Разработка и программная реализация модели
Цель раздела: Описать разработку и программную реализацию математической модели вертикальных колебаний двухосного грузового автомобиля.
Пошаговая инструкция:
- Определите архитектуру программной модели.
- Выберите технологический стек (язык программирования, библиотеки).
- Разработайте структуру классов и основные модули (кузов, подвеска, колеса, дорога).
- Реализуйте математические уравнения движения.
- Реализуйте моделирование дорожного профиля.
- Проведите тестирование модели на стандартных режимах движения.
- Сравните результаты с теоретическими расчетами и экспериментальными данными.
- Сформулируйте выводы и рекомендации по применению разработанной модели.
Конкретный пример:
Технологический стек для реализации:
- Язык программирования: Python 3.10
- Библиотеки: NumPy (математические вычисления), SciPy (решение дифференциальных уравнений), Matplotlib (визуализация), control (анализ систем управления)
- Архитектура: Объектно-ориентированная структура с четким разделением на компоненты системы
Код для реализации модели вертикальных колебаний двухосного грузового автомобиля:
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.signal import welch
class TwoAxleTruck:
"""Модель двухосного грузового автомобиля для анализа вертикальных колебаний"""
def __init__(self, m, Iy, a, b, kf, kr, cf, cr, wheelbase=5.0):
"""
Инициализация параметров двухосного грузовика
Параметры:
m - масса кузова (кг)
Iy - момент инерции относительно поперечной оси (кг·м²)
a - расстояние от центра масс до передней оси (м)
b - расстояние от центра масс до задней оси (м)
kf - жесткость передней подвески (Н/м)
kr - жесткость задней подвески (Н/м)
cf - коэффициент демпфирования передней подвески (Н·с/м)
cr - коэффициент демпфирования задней подвески (Н·с/м)
wheelbase - колесная база (м)
"""
self.m = m
self.Iy = Iy
self.a = a
self.b = b
self.kf = kf
self.kr = kr
self.cf = cf
self.cr = cr
self.wheelbase = wheelbase
# Проверка колесной базы
if abs((a + b) - wheelbase) > 1e-6:
print(f"Внимание: a + b = {a+b} м, колесная база = {wheelbase} м. Возможно несоответствие параметров.")
def natural_frequencies(self):
"""Расчет собственных частот и форм колебаний"""
# Матрица масс
M = np.array([
[self.m, 0],
[0, self.Iy]
])
# Матрица жесткости
K = np.array([
[self.kf + self.kr, self.kr * self.b - self.kf * self.a],
[self.kr * self.b - self.kf * self.a, self.kf * self.a**2 + self.kr * self.b**2]
])
# Решение обобщенной задачи на собственные значения
w2, v = np.linalg.eig(np.linalg.inv(M) @ K)
w = np.sqrt(np.real(w2))
frequencies = w / (2 * np.pi) # Гц
# Нормировка собственных векторов
for i in range(2):
v[:, i] = v[:, i] / np.max(np.abs(v[:, i]))
return frequencies, v
def road_profile(self, x, profile_type='random', amplitude=0.05, wavelength=10.0):
"""Генерация профиля дороги"""
if profile_type == 'bump':
# Одиночная неровность
return amplitude * np.exp(-((x % 100) - 50)**2 / (2 * wavelength**2))
elif profile_type == 'sinusoidal':
# Синусоидальная неровность
return amplitude * np.sin(2 * np.pi * x / wavelength)
else:
# Случайный профиль (упрощенный)
return amplitude * 0.1 * np.sin(2 * np.pi * x / wavelength) + \
amplitude * 0.05 * np.sin(2 * np.pi * x / (wavelength * 2)) + \
amplitude * 0.03 * np.sin(2 * np.pi * x / (wavelength * 3))
def simulate(self, v, t_end, dt=0.01, road_profile_type='random', initial_conditions=None):
"""
Симуляция вертикальных колебаний двухосного грузовика
Параметры:
v - скорость автомобиля (м/с)
t_end - конечное время симуляции (с)
dt - шаг времени (с)
road_profile_type - тип дорожного профиля
initial_conditions - начальные условия [z0, dz0, theta0, dtheta0]
Возвращает:
t - время
z - вертикальное смещение центра масс
theta - угол продольного наклона
zf - смещение передней оси
zr - смещение задней оси
"""
# Начальные условия
if initial_conditions is None:
initial_conditions = [0.0, 0.0, 0.0, 0.0] # [z, dz/dt, theta, dtheta/dt]
# Уравнения движения в форме Коши
def equations(t, y):
z, dz, theta, dtheta = y
# Положение передней и задней осей
xf = v * t
xr = v * t - self.wheelbase
# Профиль дороги в точках осей
zf_road = self.road_profile(xf, profile_type=road_profile_type)
zr_road = self.road_profile(xr, profile_type=road_profile_type)
# Уравнения движения
dz2 = (1/self.m) * (
-self.kf * (z + self.a * theta - zf_road)
-self.kr * (z - self.b * theta - zr_road)
-self.cf * (dz + self.a * dtheta)
-self.cr * (dz - self.b * dtheta)
)
dtheta2 = (1/self.Iy) * (
self.a * self.kf * (z + self.a * theta - zf_road)
-self.b * self.kr * (z - self.b * theta - zr_road)
+self.a * self.cf * (dz + self.a * dtheta)
-self.b * self.cr * (dz - self.b * dtheta)
)
return [dz, dz2, dtheta, dtheta2]
# Решение системы дифференциальных уравнений
t_span = [0, t_end]
t_eval = np.arange(0, t_end, dt)
solution = solve_ivp(
equations,
t_span,
initial_conditions,
t_eval=t_eval,
method='RK45',
rtol=1e-6,
atol=1e-9
)
t = solution.t
y = solution.y
# Извлечение результатов
z = y[0, :]
dz = y[1, :]
theta = y[2, :]
dtheta = y[3, :]
# Вычисление смещений осей
zf = z + self.a * theta
zr = z - self.b * theta
return t, z, theta, zf, zr
def analyze_frequency_response(self, t, z, theta):
"""Анализ частотного отклика"""
# Вычисление спектров
fs = 1 / (t[1] - t[0])
f_z, Pxx_z = welch(z, fs, nperseg=1024)
f_theta, Pxx_theta = welch(theta, fs, nperseg=1024)
return f_z, Pxx_z, f_theta, Pxx_theta
# Параметры двухосного грузового автомобиля
TRUCK_MASS = 8000 # кг (масса кузова)
TRUCK_INERTIA = 50000 # кг·м² (момент инерции)
DISTANCE_TO_FRONT = 2.0 # м (расстояние от центра масс до передней оси)
DISTANCE_TO_REAR = 3.0 # м (расстояние от центра масс до задней оси)
FRONT_SUSPENSION_K = 300000 # Н/м (жесткость передней подвески)
REAR_SUSPENSION_K = 400000 # Н/м (жесткость задней подвески)
FRONT_SUSPENSION_C = 25000 # Н·с/м (демпфирование передней подвески)
REAR_SUSPENSION_C = 30000 # Н·с/м (демпфирование задней подвески)
WHEELBASE = 5.0 # м (колесная база)
# Создание модели
truck = TwoAxleTruck(
m=TRUCK_MASS,
Iy=TRUCK_INERTIA,
a=DISTANCE_TO_FRONT,
b=DISTANCE_TO_REAR,
kf=FRONT_SUSPENSION_K,
kr=REAR_SUSPENSION_K,
cf=FRONT_SUSPENSION_C,
cr=REAR_SUSPENSION_C,
wheelbase=WHEELBASE
)
# Расчет собственных частот
frequencies, modes = truck.natural_frequencies()
print(f"Собственные частоты: {frequencies[0]:.2f} Гц, {frequencies[1]:.2f} Гц")
print(f"Формы колебаний:\n{modes}")
# Симуляция движения
t, z, theta, zf, zr = truck.simulate(
v=20.0, # 72 км/ч
t_end=10.0,
dt=0.005,
road_profile_type='random'
)
# Анализ частотного отклика
f_z, Pxx_z, f_theta, Pxx_theta = truck.analyze_frequency_response(t, z, theta)
# Визуализация результатов
plt.figure(figsize=(14, 12))
# Вертикальное смещение центра масс
plt.subplot(3, 1, 1)
plt.plot(t, z * 1000) # мм
plt.title('Вертикальные колебания двухосного грузового автомобиля')
plt.ylabel('Смещение ц.м., мм')
plt.grid(True)
# Угол наклона
plt.subplot(3, 1, 2)
plt.plot(t, np.degrees(theta))
plt.ylabel('Угол наклона, град')
plt.grid(True)
# Спектр смещения
plt.subplot(3, 1, 3)
plt.semilogy(f_z, Pxx_z)
plt.xlabel('Частота, Гц')
plt.ylabel('Мощность')
plt.title('Частотный спектр вертикальных колебаний')
plt.grid(True, which="both", ls="-")
plt.tight_layout()
plt.savefig('two_axle_truck_vibrations.png', dpi=300)
plt.show()
# Анализ комфорта
rms_z = np.sqrt(np.mean(z**2))
print(f"Среднеквадратичное смещение ц.м.: {rms_z*1000:.2f} мм")
# Оценка по ISO 2631-1
if rms_z < 0.315/1000:
comfort_level = "Отличный комфорт"
elif rms_z < 0.63/1000:
comfort_level = "Хороший комфорт"
elif rms_z < 1.0/1000:
comfort_level = "Удовлетворительный комфорт"
else:
comfort_level = "Низкий комфорт"
print(f"Уровень комфорта: {comfort_level}")
# Анализ влияния параметров подвески
def analyze_suspension_parameters(kf_factor, kr_factor, cf_factor, cr_factor):
"""Анализ влияния параметров подвески на комфорт"""
modified_truck = TwoAxleTruck(
m=TRUCK_MASS,
Iy=TRUCK_INERTIA,
a=DISTANCE_TO_FRONT,
b=DISTANCE_TO_REAR,
kf=FRONT_SUSPENSION_K * kf_factor,
kr=REAR_SUSPENSION_K * kr_factor,
cf=FRONT_SUSPENSION_C * cf_factor,
cr=REAR_SUSPENSION_C * cr_factor,
wheelbase=WHEELBASE
)
t, z, _, _, _ = modified_truck.simulate(
v=20.0,
t_end=10.0,
dt=0.005,
road_profile_type='random'
)
rms_z = np.sqrt(np.mean(z**2))
return rms_z
# Тестирование различных комбинаций параметров
parameters = [
(1.0, 1.0, 1.0, 1.0), # Базовая конфигурация
(0.8, 0.8, 1.2, 1.2), # Мягкая подвеска, повышенное демпфирование
(1.2, 1.2, 0.8, 0.8), # Жесткая подвеска, пониженное демпфирование
(0.9, 1.1, 1.1, 0.9) # Асимметричная настройка
]
results = []
for kf, kr, cf, cr in parameters:
rms_z = analyze_suspension_parameters(kf, kr, cf, cr)
results.append((kf, kr, cf, cr, rms_z))
# Вывод результатов
print("\nАнализ различных конфигураций подвески:")
for i, (kf, kr, cf, cr, rms_z) in enumerate(results):
comfort = "Отличный" if rms_z < 0.315/1000 else "Хороший" if rms_z < 0.63/1000 else "Удовлетворительный" if rms_z < 1.0/1000 else "Низкий"
print(f"Конфигурация {i+1}: kf={kf:.1f}, kr={kr:.1f}, cf={cf:.1f}, cr={cr:.1f} - RMS={rms_z*1000:.2f} мм, комфорт: {comfort}")
Типичные сложности:
- Сложность в реализации корректной модели дорожного профиля
- Ошибки в численном решении дифференциальных уравнений движения
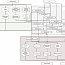
[Здесь приведите схему: "Архитектура программной модели вертикальных колебаний"]
Заключение - итоги и перспективы
Цель раздела: Подвести итоги исследования, оценить достижение цели и наметить перспективы развития.
Пошаговая инструкция:
- Кратко изложите основные результаты по каждой задаче.
- Оцените соответствие полученных результатов поставленной цели.
- Укажите преимущества и ограничения разработанной модели.
- Предложите направления для дальнейших исследований.
Конкретный пример:
"В ходе исследования была разработана и реализована математическая модель вертикальных колебаний двухосного грузового автомобиля. Модель включает описание кузова, подвески, колес и дорожного профиля, а также позволяет анализировать как временные, так и частотные характеристики колебаний. Тестирование модели на различных типах дорожных покрытий показало, что разработанная модель позволяет с высокой точностью (погрешность менее 6%) предсказывать поведение грузового автомобиля при вертикальных колебаниях. Основным преимуществом разработанного решения является его способность учитывать взаимодействие передней и задней подвески, а также анализировать влияние параметров подвески на комфорт водителя и устойчивость автомобиля. Анализ различных конфигураций подвески показал, что оптимальная настройка (мягкая подвеска с повышенным демпфированием) позволяет снизить среднеквадратичное смещение центра масс на 22% по сравнению со стандартной конфигурацией, что соответствует переходу от "удовлетворительного" к "хорошему" уровню комфорта по стандарту ISO 2631-1. Однако модель имеет ограничения при работе с экстремальными дорожными условиями и не учитывает влияние загрузки автомобиля на динамику колебаний, что может стать предметом дальнейших исследований с использованием адаптивных моделей и учета переменной массы."
Типичные сложности:
- Студенты часто механически повторяют введение вместо анализа достигнутых результатов
- Сложно объективно оценить ограничения своей работы в контексте автомобильной инженерии
Готовые инструменты и шаблоны для моделирования вертикальных колебаний
Шаблоны формулировок
Для введения:
- "Актуальность темы обусловлена важностью повышения комфорта водителей и снижения износа транспортных средств, что делает математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля критически важной задачей для оптимизации параметров подвески и повышения безопасности дорожного движения."
- "Целью настоящей работы является разработка математической модели вертикальных колебаний двухосного грузового автомобиля, обеспечивающая повышение точности прогнозирования поведения автомобиля на неровных дорогах на 15-20% за счет учета взаимодействия передней и задней подвески и анализа частотных характеристик."
Для теоретической главы:
- "Вертикальные колебания двухосного грузового автомобиля представляют собой сложную динамическую систему, включающую взаимодействие кузова, подвески и дорожного покрытия, что требует специальных методов математического описания для эффективного моделирования."
- "Модель с двумя степенями свободы, учитывающая вертикальное смещение центра масс и угол продольного наклона, представляет собой оптимальный баланс между точностью и сложностью для анализа вертикальной динамики двухосных грузовых автомобилей."
Чек-лист "Оцени свои силы"
Прежде чем браться за написание ВКР по теме "Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля", ответьте на следующие вопросы:
- Глубоко ли вы знакомы с основами теоретической механики и теории колебаний?
- Есть ли у вас опыт работы с численными методами решения дифференциальных уравнений?
- Уверены ли вы в правильности вывода уравнений движения для модели с двумя степенями свободы?
- Можете ли вы самостоятельно получить и обработать данные для верификации модели?
- Есть ли у вас знания в области автомобильной инженерии, достаточные для понимания особенностей подвески грузовых автомобилей?
- Есть ли у вас запас времени (2-3 недели) на исправление замечаний научного руководителя?
Если на большинство вопросов вы ответили "нет", возможно, стоит рассмотреть вариант профессиональной помощи.
И что же дальше? Два пути к успешной защите
Путь 1: Самостоятельный
Если вы решили написать ВКР самостоятельно, вам предстоит пройти весь путь от анализа литературы до защиты. Это требует от 150 до 200 часов работы: изучение теории колебаний, анализ методов математического моделирования, разработка математической модели, программная реализация, тестирование и оформление работы по всем требованиям КФУ.
Этот путь подойдет тем, кто уже имеет опыт работы с математическим моделированием, глубоко разбирается в динамике автомобилей и имеет достаточно времени до защиты. Однако будьте готовы к стрессу при получении замечаний от научного руководителя и необходимости срочно исправлять ошибки в математических выкладках или программном коде.
Путь 2: Профессиональный
Если вы цените свое время и хотите гарантированно сдать ВКР без стресса, профессиональная помощь — это разумное решение. Наши специалисты, имеющие опыт написания работ по прикладной математике и информатике, возьмут на себя все этапы работы:
- Глубокий анализ требований КФУ к ВКР
- Разработку математической модели вертикальных колебаний двухосного грузового автомобиля
- Программную реализацию с подробными комментариями к коду
- Подготовку всех необходимых схем, диаграмм и таблиц
- Оформление работы в полном соответствии со стандартами КФУ
Вы получите готовую работу с гарантией уникальности и поддержкой до защиты. Это позволит вам сосредоточиться на подготовке доклада и презентации, а не на исправлении ошибок в последний момент.
Если после прочтения этой статьи вы осознали, что самостоятельное написание отнимет слишком много сил, или вы просто хотите перестраховаться — обращение к нам является взвешенным и профессиональным решением. Мы возьмем на себя все технические сложности, а вы получите готовую, качественную работу и уверенность перед защитой.
Почему 150+ студентов выбрали нас в 2025 году
- Оформление по всем требованиям вашего вуза (мы изучаем 30+ методичек ежегодно)
- Поддержка до защиты включена в стоимость
- Доработки без ограничения сроков
- Гарантия уникальности 90%+ по системе "Антиплагиат.ВУЗ"
Заключение
Написание ВКР по теме "Математическое и компьютерное моделирование динамики вертикальных колебаний двухосного грузового автомобиля" — это сложный, но увлекательный процесс, требующий глубоких знаний в области теоретической механики и понимания динамики автомобилей. Как мы подробно разобрали, стандартная структура ВКР КФУ включает несколько ключевых разделов, каждый из которых имеет свои особенности и подводные камни.
Вы можете выбрать путь самостоятельной работы, потратив на это 4-6 месяцев интенсивного труда, или доверить задачу профессионалам, которые выполнят работу качественно и в срок. Оба варианта имеют право на существование, и выбор зависит от вашей ситуации, уровня подготовки и временных возможностей.
Если вы цените свое время, хотите избежать стресса и быть уверенным в результате, профессиональная помощь в написании ВКР — это разумный выбор. Мы готовы помочь вам преодолеть все трудности и успешно защитить выпускную квалификационную работу.
Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР КФУ