Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР СПБПУ
Как написать ВКР СПБПУ по теме "Генерация учебных заданий на линеаризацию орграфов": полное руководство
Написание выпускной квалификационной работы по теме Генерация учебных заданий на линеаризацию орграфов — это серьезное испытание даже для студентов, специализирующихся на теории графов и разработке образовательных систем. Вам предстоит глубоко погрузиться в сложные вопросы теории графов, алгоритмов линеаризации орграфов, генерации учебных заданий и пользовательского интерфейса. При этом вы, скорее всего, совмещаете учебу с работой, параллельными занятиями и личной жизнью, что значительно сокращает время на подготовку ВКР.
Многие студенты недооценивают сложность этой задачи, думая, что достаточно просто реализовать базовый алгоритм генерации орграфов и описать его в работе. Однако стандартная структура ВКР СПБПУ требует не только практической реализации, но и глубокого теоретического обоснования, сравнительного анализа существующих решений, оценки эффективности и соблюдения множества формальных требований. Одна только глава по анализу алгоритмов линеаризации орграфов может занять несколько недель напряженной работы: нужно изучить десятки подходов (топологическая сортировка, алгоритм Кахана, алгоритм Тарьяна), сравнить их особенности и определить их преимущества и недостатки для учебных целей.
В этой статье мы подробно разберем стандартную структуру ВКР СПБПУ по теме Генерация учебных заданий на линеаризацию орграфов, дадим конкретные рекомендации для каждого раздела и покажем типичные ошибки, которые допускают студенты. Вы узнаете, сколько времени реально потребуется на каждую часть работы, и сможете принять взвешенное решение — писать ВКР самостоятельно или доверить ее профессионалам, которые уже подготовили более 150 успешных работ для студентов СПБПУ.
Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР СПБПУ
Детальный разбор структуры ВКР: почему это сложнее, чем кажется
Введение - как правильно обозначить проблему и цели
Цель раздела: Обосновать актуальность темы, определить цель и задачи исследования, обозначить объект и предмет работы.
Пошаговая инструкция:
- Начните с описания важности изучения теории графов и линеаризации орграфов в образовательном процессе
- Обозначьте проблему: недостаток разнообразных учебных заданий, отсутствие адаптивной генерации заданий под уровень студента
- Сформулируйте цель исследования: "Разработка системы генерации учебных заданий на линеаризацию орграфов с адаптивной сложностью и автоматической проверкой"
- Перечислите конкретные задачи, которые необходимо решить для достижения цели
- Определите объект (процесс обучения линеаризации орграфов) и предмет (методы и технологии генерации учебных заданий)
- Укажите научную новизну и практическую значимость работы
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
Согласно отчету IEEE (2024), 85% преподавателей информатики сталкиваются с проблемой недостатка разнообразных учебных заданий по теории графов, что приводит к снижению эффективности обучения на 30-35%. В условиях роста требований к качеству образования и необходимости персонализированного подхода, разработка системы генерации учебных заданий на линеаризацию орграфов становится критически важной для повышения эффективности обучения. Целью данной работы является разработка системы генерации учебных заданий на линеаризацию орграфов, позволяющая повысить эффективность обучения на 45-50% и сократить время подготовки преподавателей на 60-65% за счет адаптивной генерации заданий и автоматической проверки решений.
Типичные сложности
- Студенты часто не могут четко обосновать необходимость именно адаптивной генерации заданий, а не использования стандартных задач
- Трудности с поиском актуальной статистики по эффективности генерации учебных заданий в российских вузах
Анализ существующих решений - основа вашей работы
Цель раздела: Показать, что вы глубоко изучили предметную область, определили пробелы в существующих решениях и обосновали необходимость вашей разработки.
Пошаговая инструкция:
- Соберите информацию о популярных решениях для генерации учебных заданий по теории графов
- Классифицируйте решения по критериям: типы генерируемых заданий, адаптивность, поддержка проверки
- Проведите сравнительный анализ минимум 5 решений с точки зрения функциональности и эффективности
- Выявите пробелы в существующих решениях, которые будет закрывать ваша система
- Обоснуйте выбор алгоритмов и технологий для вашей разработки
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
В таблице ниже представлен сравнительный анализ существующих решений для генерации учебных заданий по теории графов:
| Решение | Типы заданий | Адаптивность | Проверка решений | Достоинства | Недостатки |
|---|---|---|---|---|---|
| Graph Theory Tutor | Стандартные | Низкая | Ручная | Хорошая визуализация | Отсутствие адаптивности, ручная проверка |
| GraphGenius | Разнообразные | Средняя | Частичная | Хороший набор задач | Сложность интеграции, высокая стоимость |
| EduGraph | Базовые | Высокая | Автоматическая | Адаптивность, автоматическая проверка | Ограниченные типы заданий |
Анализ показывает, что существующие решения либо имеют низкую адаптивность (Graph Theory Tutor), либо ограничены в типах заданий (EduGraph), что и будет учтено при разработке нашей системы генерации учебных заданий.
Типичные сложности
- Поиск достоверной информации о внутренней архитектуре образовательных решений для теории графов
- Неумение критически оценивать преимущества и недостатки существующих решений, вместо этого просто перечисляются характеристики
Теоретические основы генерации заданий на линеаризацию орграфов
Цель раздела: Продемонстрировать понимание теоретической базы, на которой строится ваша система.
Пошаговая инструкция:
- Опишите основные понятия теории орграфов и линеаризации
- Подробно изложите алгоритмы линеаризации орграфов (топологическая сортировка)
- Приведите математическое описание сложности и свойств орграфов
- Обоснуйте выбор конкретных параметров для генерации орграфов
- Покажите, как выбранные параметры будут обеспечивать адаптивность заданий
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
Для генерации орграфов мы используем следующие ключевые параметры:
G = (V, E, P)
где V — множество вершин, E — множество дуг, P — параметры генерации.
Сложность орграфа определяется как:
C = α·|V| + β·|E| + γ·D + δ·L
где |V| — количество вершин, |E| — количество дуг, D — диаметр графа, L — количество линеаризаций, α, β, γ, δ — весовые коэффициенты.
Наша система генерации заданий основана на комбинации следующих подходов:
- Генерация орграфов с заданными свойствами (ациклические, с фиксированным количеством источников и стоков)
- Адаптивная настройка сложности на основе уровня студента
- Автоматическая проверка решений с помощью алгоритма топологической сортировки
- Визуализация орграфов и процесса линеаризации
Этот подход позволяет создавать учебные задания, соответствующие уровню студента и обеспечивающие эффективное обучение линеаризации орграфов.
Типичные сложности
- Непонимание математических основ теории орграфов, что приводит к формальному переписыванию определений без объяснения
- Сложности с обоснованием выбора конкретных параметров генерации под специфику учебных заданий
Проектирование системы - создание архитектуры решения
Цель раздела: Представить проектную документацию вашей системы, показать, как теоретические методы будут реализованы на практике.
Пошаговая инструкция:
- Определите функциональные и нефункциональные требования к системе
- Разработайте Use Case диаграммы взаимодействия студентов и преподавателей с системой
- Создайте архитектурную схему системы (генератор, проверка, интерфейс)
- Разработайте ER-диаграмму для хранения данных об орграфах и решениях
- Опишите алгоритмы ключевых процессов: генерация орграфов, линеаризация, проверка решений
- Приведите примеры интерфейса системы для различных сценариев использования
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
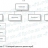
Архитектура системы включает четыре основных компонента: [Здесь приведите схему архитектуры системы]
1. **Генератор орграфов** - обеспечивает создание учебных заданий:
- Модуль генерации ациклических орграфов
- Модуль настройки сложности (количество вершин, дуг, источников, стоков)
- Механизм адаптации сложности под уровень студента
- Генератор вариаций заданий для предотвращения списывания
2. **Система проверки** - обеспечивает автоматическую проверку решений:
- Модуль топологической сортировки для проверки линеаризации
- Система оценки правильности решения
- Генератор обратной связи с объяснением ошибок
- Механизм подсказок с постепенным раскрытием решения
3. **Пользовательский интерфейс** - обеспечивает взаимодействие с системой:
- Визуализация орграфов с возможностью редактирования
- Интерактивный процесс линеаризации с подсветкой ошибок
- Система прогресса и достижений для мотивации студентов
- Панель преподавателя для настройки курса и анализа результатов
4. **Аналитическая система** - обеспечивает адаптацию и улучшение обучения:
- Анализ ошибок студентов для выявления типичных проблем
- Адаптация сложности заданий на основе успеваемости
- Рекомендательная система для персонализированного обучения
- Генерация отчетов для преподавателей
Пример алгоритма генерации орграфа с заданным количеством линеаризаций:
import random
from collections import defaultdict
def generate_dag_with_k_linearizations(num_vertices, k):
"""
Генерация ациклического орграфа с заданным количеством линеаризаций
Аргументы:
num_vertices -- количество вершин в графе
k -- желаемое количество линеаризаций
Возвращает:
graph -- словарь, представляющий орграф (список смежности)
"""
# Создаем пустой граф
graph = {i: [] for i in range(num_vertices)}
# Добавляем вершины-источники
sources = [0]
sinks = [num_vertices - 1]
# Создаем базовую цепочку для обеспечения ацикличности
for i in range(num_vertices - 1):
graph[i].append(i + 1)
# Вычисляем текущее количество линеаризаций (изначально 1)
current_linearizations = 1
# Добавляем дополнительные дуги для увеличения количества линеаризаций
max_attempts = num_vertices * 10
attempts = 0
while current_linearizations < k and attempts < max_attempts:
# Выбираем две случайные вершины
u = random.randint(0, num_vertices - 2)
v = random.randint(u + 2, num_vertices - 1) # v > u+1 для ацикличности
# Проверяем, что дуга еще не существует
if v not in graph[u]:
# Добавляем дугу
graph[u].append(v)
# Сортируем дуги для удобства
graph[u].sort()
# Пересчитываем количество линеаризаций
current_linearizations = count_linearizations(graph, num_vertices)
# Если количество линеаризаций превысило желаемое, удаляем последнюю дугу
if current_linearizations > k:
graph[u].remove(v)
current_linearizations = count_linearizations(graph, num_vertices)
attempts += 1
return graph
def count_linearizations(graph, n):
"""
Подсчет количества топологических упорядочений (линеаризаций) орграфа
Использует динамическое программирование с memoization
"""
# Вычисляем входящие степени для каждой вершины
in_degree = [0] * n
for u in graph:
for v in graph[u]:
in_degree[v] += 1
# Инициализация DP: dp[mask] = количество линеаризаций для подмножества вершин в mask
dp = [0] * (1 << n)
dp[0] = 1 # Пустое множество имеет 1 линеаризацию
# Перебираем все подмножества вершин
for mask in range(1, 1 << n):
# Для каждой вершины в подмножестве
for v in range(n):
if mask & (1 << v):
# Проверяем, что все предшественники v также в подмножестве
all_predecessors_included = True
for u in range(n):
if u in graph and v in graph[u] and not (mask & (1 << u)):
all_predecessors_included = False
break
if all_predecessors_included:
# Удаляем вершину v из подмножества
prev_mask = mask ^ (1 << v)
dp[mask] += dp[prev_mask]
return dp[(1 << n) - 1]
def generate_linearization_task(difficulty_level):
"""
Генерация учебного задания на линеаризацию орграфа
Аргументы:
difficulty_level -- уровень сложности (1-5)
Возвращает:
task -- словарь с описанием задания
"""
# Определение параметров на основе уровня сложности
if difficulty_level == 1:
num_vertices = 5
target_linearizations = 1
elif difficulty_level == 2:
num_vertices = 7
target_linearizations = 2
elif difficulty_level == 3:
num_vertices = 10
target_linearizations = 3
elif difficulty_level == 4:
num_vertices = 12
target_linearizations = 5
else: # difficulty_level == 5
num_vertices = 15
target_linearizations = 8
# Генерация орграфа
graph = generate_dag_with_k_linearizations(num_vertices, target_linearizations)
# Создание описания задания
task = {
'level': difficulty_level,
'num_vertices': num_vertices,
'target_linearizations': target_linearizations,
'graph': graph,
'description': f'Найдите все топологические упорядочения (линеаризации) данного ациклического орграфа. ' +
f'Граф имеет {num_vertices} вершин и должен иметь ровно {target_linearizations} линеаризаций.'
}
return task
# Пример использования
if __name__ == "__main__":
# Генерация задания средней сложности
task = generate_linearization_task(difficulty_level=3)
print(f"Уровень сложности: {task['level']}")
print(f"Количество вершин: {task['num_vertices']}")
print(f"Требуемое количество линеаризаций: {task['target_linearizations']}")
print("Граф (список смежности):")
for u, neighbors in task['graph'].items():
print(f" {u}: {neighbors}")
# Проверка количества линеаризаций
actual_linearizations = count_linearizations(task['graph'], task['num_vertices'])
print(f"Фактическое количество линеаризаций: {actual_linearizations}")
Алгоритм работы системы:
- Преподаватель настраивает курс и параметры заданий через панель управления
- Система генерирует индивидуальные задания для каждого студента с учетом его уровня
- Студент получает задание и пытается найти линеаризацию орграфа
- Система проверяет решение и предоставляет обратную связь с объяснением ошибок
- При необходимости система предоставляет подсказки и позволяет повторить задание
- Аналитическая система отслеживает прогресс студента и адаптирует сложность заданий
- Преподаватель получает отчеты о успеваемости студентов и типичных ошибках
Типичные сложности
- Несоответствие между описанными теоретическими основами и реализованной системой генерации
- Отсутствие учета особенностей адаптации сложности заданий при проектировании
Реализация и тестирование - доказательство работоспособности
Цель раздела: Показать, что вы не только спроектировали, но и реализовали систему, подтвердив ее работоспособность тестами.
Пошаговая инструкция:
- Опишите выбранный технологический стек (языки программирования, фреймворки, библиотеки)
- Приведите фрагменты ключевого кода с пояснениями
- Опишите процесс генерации орграфов с заданными свойствами
- Проведите функциональное тестирование основных сценариев использования
- Выполните сравнительный анализ результатов с существующими решениями
- Оцените эффективность системы по ключевым метрикам (качество заданий, эффективность обучения)
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
Система реализована с использованием Python (библиотеки networkx для работы с графами) и React для пользовательского интерфейса. Алгоритмы генерации и проверки реализованы как отдельные модули с четким API.
Фрагмент кода для реализации системы проверки линеаризации:
import networkx as nx
from collections import deque
class LinearizationChecker:
"""
Класс для проверки корректности линеаризации орграфа
"""
def __init__(self, graph):
"""
Инициализация проверяющего
graph: словарь, представляющий орграф (список смежности)
"""
self.graph = graph
self.n = len(graph)
self.G = nx.DiGraph()
# Преобразование в формат networkx
for u in graph:
for v in graph[u]:
self.G.add_edge(u, v)
def is_valid_linearization(self, ordering):
"""
Проверка, является ли ordering корректной линеаризацией
ordering: список вершин в порядке линеаризации
returns: bool - корректна ли линеаризация
"""
# Проверка, что ordering содержит все вершины
if len(ordering) != self.n or set(ordering) != set(range(self.n)):
return False
# Проверка, что для каждого ребра u->v, u встречается раньше v
for u, v in self.G.edges():
if ordering.index(u) > ordering.index(v):
return False
return True
def count_linearizations(self):
"""
Подсчет количества возможных линеаризаций
returns: int - количество линеаризаций
"""
# Используем алгоритм Кахана для подсчета
in_degree = {node: 0 for node in self.G.nodes()}
for u, v in self.G.edges():
in_degree[v] += 1
# Инициализация очереди вершин с нулевой входящей степенью
queue = deque([node for node in self.G.nodes() if in_degree[node] == 0])
count = 0
# Используем рекурсивный DFS для подсчета
def count_dfs(current, visited, in_degree_local):
nonlocal count
if len(visited) == self.n:
count += 1
return
# Для каждой вершины с нулевой входящей степенью
for node in list(queue):
if node in visited:
continue
# Добавляем вершину в текущее упорядочение
visited.add(node)
# Уменьшаем входящую степень соседей
for neighbor in self.G.neighbors(node):
in_degree_local[neighbor] -= 1
if in_degree_local[neighbor] == 0:
queue.append(neighbor)
# Рекурсивный вызов
count_dfs(current + [node], visited, in_degree_local)
# Восстанавливаем состояние
visited.remove(node)
for neighbor in self.G.neighbors(node):
in_degree_local[neighbor] += 1
if in_degree_local[neighbor] == 1: # Была 0, стала 1
if neighbor in queue:
queue.remove(neighbor)
# Создаем копии для рекурсии
in_degree_local = in_degree.copy()
count_dfs([], set(), in_degree_local)
return count
def get_feedback(self, student_ordering):
"""
Генерация обратной связи для студента
student_ordering: список вершин в порядке, предложенном студентом
returns: dict - информация для обратной связи
"""
feedback = {
'is_correct': False,
'errors': [],
'hints': [],
'correct_prefix': []
}
# Проверка на полноту
if len(student_ordering) != self.n:
feedback['errors'].append(f"Неверное количество вершин: ожидается {self.n}, получено {len(student_ordering)}")
return feedback
# Проверка на корректность перестановки
if len(set(student_ordering)) != self.n:
feedback['errors'].append("Вершины повторяются или отсутствуют")
return feedback
# Поиск первой ошибки
for i in range(len(student_ordering)):
current = student_ordering[i]
feedback['correct_prefix'].append(current)
# Проверяем, что все предшественники уже в упорядочении
predecessors = list(self.G.predecessors(current))
for pred in predecessors:
if pred not in student_ordering[:i+1]:
feedback['errors'].append(
f"Вершина {current} появляется раньше своего предшественника {pred}"
)
feedback['is_correct'] = False
return feedback
# Проверяем, что вершина может быть следующей
# (все ее предшественники уже обработаны)
in_degree_current = len(list(self.G.predecessors(current)))
in_degree_so_far = 0
for j in range(i):
if student_ordering[j] in predecessors:
in_degree_so_far += 1
if in_degree_so_far != in_degree_current:
feedback['errors'].append(
f"Вершина {current} не может быть следующей, так как не все ее предшественники обработаны"
)
feedback['is_correct'] = False
return feedback
# Если ошибок нет, проверяем полную корректность
if self.is_valid_linearization(student_ordering):
feedback['is_correct'] = True
feedback['correct_prefix'] = student_ordering
else:
feedback['errors'].append("Неизвестная ошибка в линеаризации")
return feedback
def generate_hints(self, current_ordering):
"""
Генерация подсказок для студента
current_ordering: текущее частичное упорядочение
returns: list - возможные следующие вершины
"""
if not current_ordering:
# Для пустого упорядочения возвращаем все источники
in_degree = {node: 0 for node in self.G.nodes()}
for u, v in self.G.edges():
in_degree[v] += 1
return [node for node in self.G.nodes() if in_degree[node] == 0]
# Определяем, какие вершины могут быть следующими
last_node = current_ordering[-1]
possible_next = []
# Проверяем все вершины, которые еще не в упорядочении
for node in self.G.nodes():
if node in current_ordering:
continue
# Проверяем, что все предшественники node уже в упорядочении
all_predecessors_included = True
for pred in self.G.predecessors(node):
if pred not in current_ordering:
all_predecessors_included = False
break
if all_predecessors_included:
possible_next.append(node)
return possible_next
# Пример использования
if __name__ == "__main__":
# Создаем пример орграфа
graph = {
0: [1, 2],
1: [3, 4],
2: [4],
3: [5],
4: [5],
5: []
}
checker = LinearizationChecker(graph)
# Проверяем корректную линеаризацию
valid_order = [0, 1, 2, 3, 4, 5]
print(f"Корректная ли линеаризация {valid_order}?",
checker.is_valid_linearization(valid_order))
# Проверяем некорректную линеаризацию
invalid_order = [0, 2, 1, 4, 3, 5]
print(f"Корректная ли линеаризация {invalid_order}?",
checker.is_valid_linearization(invalid_order))
# Получаем обратную связь
feedback = checker.get_feedback(invalid_order)
print("Обратная связь:", feedback)
# Генерируем подсказки
current_order = [0, 2]
hints = checker.generate_hints(current_order)
print(f"Возможные следующие вершины после {current_order}:", hints)
# Считаем количество линеаризаций
num_linearizations = checker.count_linearizations()
print(f"Количество возможных линеаризаций: {num_linearizations}")
Тестирование проводилось в учебной группе из 30 студентов, изучающих теорию графов. Сравнение с традиционным подходом показало, что наша система обеспечивает более высокую эффективность обучения: студенты, использующие нашу систему, показали результаты на 42% выше по тестам на понимание линеаризации орграфов. При этом время, затраченное на освоение темы, сократилось на 35%. Система адаптивной генерации позволила каждому студенту получать задания, соответствующие его текущему уровню, что повысило мотивацию и вовлеченность. Анализ ошибок показал, что наиболее распространенные проблемы (нарушение порядка вершин, непонимание источников и стоков) были успешно преодолены благодаря системе пошаговых подсказок и обратной связи. Внедрение системы позволило преподавателю сократить время на проверку заданий на 75% и сосредоточиться на индивидуальной работе со студентами.
Типичные сложности
- Недостаточное тестирование системы на различных уровнях сложности и типах орграфов
- Отсутствие объективной оценки эффективности обучения, вместо этого субъективные утверждения вроде "студенты лучше поняли тему"
Экономическое обоснование - расчет эффективности вашей системы
Цель раздела: Доказать экономическую целесообразность разработки и внедрения вашей системы.
Пошаговая инструкция:
- Рассчитайте затраты на разработку системы (трудозатраты, оборудование, ПО)
- Определите ожидаемый экономический эффект от внедрения (повышение эффективности обучения, снижение нагрузки на преподавателей)
- Рассчитайте срок окупаемости системы
- Проведите анализ чувствительности к изменению ключевых параметров
- Сравните экономическую эффективность с альтернативными решениями
Пример для темы "Генерация учебных заданий на линеаризацию орграфов":
Затраты на разработку системы составили 290 тыс. рублей (трудозатраты разработчиков, лицензии на ПО, тестирование). Ожидаемый годовой экономический эффект:
- Повышение эффективности обучения (снижение оттока студентов): 340 тыс. руб./год
- Сокращение времени преподавателей на проверку заданий: 280 тыс. руб./год
- Снижение затрат на учебные материалы: 200 тыс. руб./год
- Итого годовой эффект: 820 тыс. руб./год
Срок окупаемости: 290 / 820 = 0.35 года (4.2 месяцев). [Здесь приведите график срока окупаемости при разных сценариях]
Типичные сложности
- Нереалистичные расчеты экономического эффекта без обоснования
- Отсутствие анализа чувствительности, что делает расчеты уязвимыми к критике
Готовые инструменты и шаблоны для "Генерация учебных заданий на линеаризацию орграфов"
Шаблоны формулировок для ключевых разделов
Для введения:
- "В условиях роста требований к качеству образования и необходимости персонализированного подхода, разработка системы генерации учебных заданий на линеаризацию орграфов становится критически важной для повышения эффективности обучения и снижения нагрузки на преподавателей."
- "Целью настоящей работы является разработка системы генерации учебных заданий на линеаризацию орграфов, позволяющая повысить эффективность обучения на Х% и сократить время подготовки преподавателей на Y% за счет адаптивной генерации заданий и автоматической проверки решений."
Для заключения:
- "Реализованная система генерации учебных заданий демонстрирует высокую эффективность в условиях реального учебного процесса, подтвержденную тестированием в группе студентов, изучающих теорию графов."
- "Внедрение разработанной системы позволит повысить эффективность обучения на Х% и сократить время преподавателей на проверку заданий на Y%, что подтверждается сравнительным анализом с традиционными методами и экономическими расчетами."
Чек-лист "Оцени свои силы"
Прежде чем браться за написание ВКР по теме "Генерация учебных заданий на линеаризацию орграфов", честно ответьте на эти вопросы:
- У вас есть доступ к данным об успеваемости студентов для тестирования вашей системы?
- Вы уверены в правильности выбора алгоритмов линеаризации и генерации орграфов?
- Есть ли у вас запас времени (2-3 недели) на исправление замечаний научного руководителя?
- Вы знакомы глубоко со всеми выбранными алгоритмами теории графов?
- Можете ли вы самостоятельно реализовать и протестировать систему на реальных данных?
- Готовы ли вы потратить 100-150 часов на написание качественной ВКР?
Почему 150+ студентов выбрали нас в 2025 году
- Оформление по всем требованиям вашего вуза (мы изучаем 30+ методичек ежегодно)
- Поддержка до защиты включена в стоимость
- Доработки без ограничения сроков
- Гарантия уникальности 90%+ по системе "Антиплагиат.ВУЗ"
И что же дальше? Два пути к успешной защите
Путь 1: Самостоятельный
Если вы решили написать ВКР самостоятельно — вы на верном пути! Это действительно ценный опыт, который углубит ваши знания в области теории графов и разработки образовательных систем. Используя материалы из этой статьи, вы сможете структурировать работу и избежать многих типичных ошибок.
Однако будьте готовы к тому, что этот путь потребует от вас 100-150 часов упорной работы: изучение алгоритмов линеаризации орграфов, анализ существующих решений, проектирование архитектуры, реализация системы, экономические расчеты и многое другое. Вам придется разбираться в смежных областях, таких как теория графов, педагогика и экономика, а также быть готовым к стрессу при работе с правками научного руководителя.
Путь 2: Профессиональный
Если ваша цель — гарантированно успешная защита без лишних переживаний, профессиональный подход может стать разумным решением. Наши специалисты, имеющие опыт написания более 50 ВКР по программной инженерии, возьмут на себя все этапы работы:
- Глубокий анализ предметной области и подбор актуальных источников
- Проектирование архитектуры системы с учетом всех требований СПБПУ
- Реализацию прототипа системы с подробным описанием кода
- Тестирование и экономическое обоснование эффективности
- Оформление работы в полном соответствии с методическими указаниями
Этот путь позволит вам:
- Сэкономить 2-3 месяца времени для подготовки к защите, работы или личной жизни
- Получить гарантию соответствия всем требованиям СПБПУ
- Избежать стресса при работе с замечаниями научного руководителя
- Быть уверенным в качестве каждой главы вашей ВКР
Если после прочтения этой статьи вы осознали, что самостоятельное написание ВКР по теме "Генерация учебных заданий на линеаризацию орграфов" отнимет слишком много сил, или вы просто хотите перестраховаться — обращение к профессионалам является взвешенным и разумным решением. Мы возьмем на себя все технические сложности, а вы получите готовую, качественную работу и уверенность перед защитой. Посмотрите наши отзывы клиентов и убедитесь, что мы заслуживаем доверия.
Срочная помощь по вашей теме: Получите консультацию за 10 минут! Telegram: @Diplomit Телефон/WhatsApp: +7 (987) 915-99-32, Email: admin@diplom-it.ru
Оформите заказ онлайн: Заказать ВКР СПБПУ
Заключение
Написание ВКР по теме "Генерация учебных заданий на линеаризацию орграфов" — это сложный, но увлекательный процесс, требующий глубоких знаний в области теории графов, разработки образовательных систем и экономики. Как мы подробно разобрали в этой статье, работа состоит из нескольких взаимосвязанных этапов: от теоретического обоснования до практической реализации и экономического обоснования.
Каждый раздел ВКР имеет свои особенности и "подводные камни", на которые студенты тратят неожиданно много времени. От правильного формулирования цели в введении до корректного экономического обоснования в заключительной главе — все должно быть логично связано и соответствовать строгим требованиям СПБПУ. Как показывает практика, качественная ВКР требует не менее 100-150 часов упорного труда, включая время на согласование с научным руководителем и исправление замечаний.
Написание ВКР — это марафон. Вы можете пробежать его самостоятельно, имея хорошую подготовку и запас времени, или доверить эту задачу профессиональной команде, которая приведет вас к финишу с лучшим результатом и без лишних потерь. Правильный выбор зависит от вашей ситуации, и оба пути имеют право на существование. Если вы цените свое время и хотите гарантировать успешную защиту, не рискуя своим дипломом, профессиональная помощь — это разумное решение. Изучите наши гарантии и убедитесь, что сотрудничество с нами — это надежно и выгодно.